Tris par insertion et par sélection

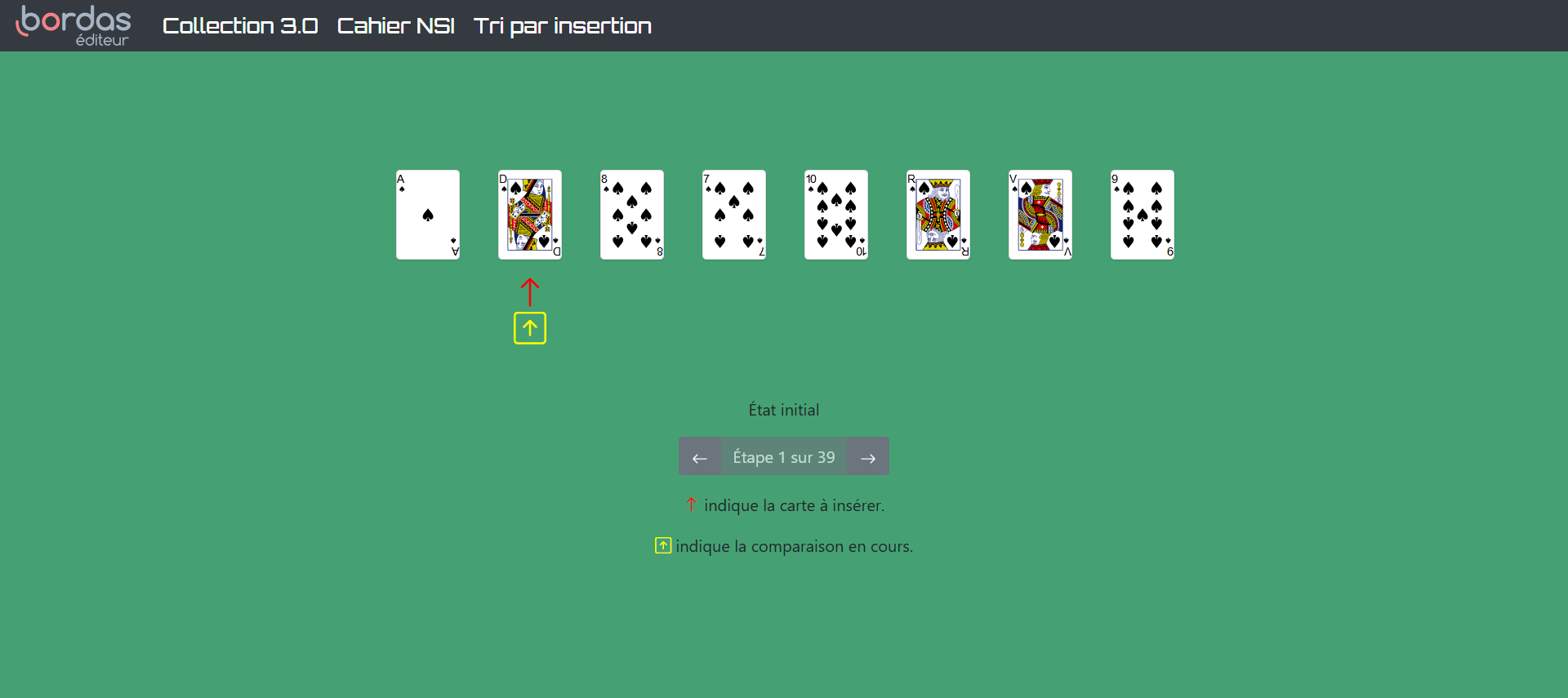
Le tri par insertion⚓︎

Il s’agit de l’algorithme « naturel » que l’on applique pour trier des cartes par ordre croissant.

Principe⚓︎

On peut traduire l’algorithme de tri par insertion de la façon suivante :

Prendre le 2ème élément du tableau et l’insérer à sa place parmi ceux qui le précèdent
Prendre le 3ème élément du tableau et l’insérer à sa place parmi ceux qui le précèdent
Continuer ainsi jusqu'à ce que le tableau soit entièrement trié.

Algorithme en pseudocode⚓︎

Pseudocode

// En pseudocode, les indices d'un tableau T vont de 1 à n
pour i de 2 à n faire
    x ← T[i]
    j ← i
    tant que j > 1 et x < T[j-1] faire
        T[j] ← T[j-1]
        j ← j – 1
    fin tant que
    T[j] ← x
fin pour

Efficacité de l’algorithme⚓︎

On rappelle que l’efficacité d’un algorithme correspond à son coût en terme d’opérations élémentaires dans le pire cas. Pour simplifier cette étude, on ne va étudier ici que le nombre de comparaisons du tri par insertion.

Qu’est-ce que le pire cas ? Un tableau trié par ordre décroissant puisqu’il faut aller insérer chaque élément en première position : cela implique de le comparer à tous ceux qui le précèdent.

Pour un tableau de taille n trié par ordre décroissant (pire cas), on a :

Au 1er passage dans la boucle (\(i = 2\)), il y a \(1\) comparaison à faire : \(T[2]\) avec \(T[1]\) ;
Au 2ème passage (\(i = 3\)), il y a \(2\) comparaisons à faire : \(T[3]\) avec successivement \(T[2]\) et \(T[1]\) ;
Ainsi de suite ...;
Au dernier passage (\(i = n\)), il y a \(n – 1\) comparaisons à faire : \(T[n]\) avec successivement à \(T[n-1]\), \(T[n-2]\), ..., \(T[1]\)).

Il y a donc en tout \(1 + 2 + 3 + ... + (n - 2) + (n - 1)\) comparaisons dans le pire cas.
Or, on peut démontrer que : \(1 + 2 + 3 + ... + (n - 2) + (n - 1) = \dfrac{n (n - 1)}{2} = \dfrac{n^2}{2} - \dfrac{n}{2}\)

Complexité temporelle⚓︎

Complexité du tri par insertion

On peut alors dire que le coût de l’algorithme est de l’ordre de \(n^2\) (on prend la plus grande puissance de \(n\)) ou que sa complexité temporelle est en \(O(n^2)\).

On dit que l’algorithme de tri par insertion a un coût quadratique.

Cela signifie que :

si l’on double la taille du tableau \(T\), alors le temps de calcul (théorique) n’est pas doublé mais est multiplié par \(2^2 = 4\) ;
si on triple la taille de \(T\), le temps de calcul (théorique) est multiplié par \(3^2 = 9\) ;
etc.

Tri par insertion (animation Bordas)

Vidéo de Cédric Gerland (15:11)

Invariant de boucle⚓︎

Un invariant de boucle est une propriété qui reste vraie avant et après chaque itération de la boucle. Pour cet algorithme, l'invariant de boucle peut être formulé comme suit :

Invariant : à chaque début d'itération de la boucle externe « pour », le sous-tableau \(T[1..i-1]\) est trié.

Preuve de l'invariant de boucle :

Initialisation : avant la première itération (\(i = 2\)), le sous-tableau \(T[1..1]\) contient un seul élément, donc il est trivialement trié.

Conservation : supposons que l'invariant est vrai au début de l'itération pour un certain \(i\). L'élément \(x\) est initialisé avec \(T[i]\), et on doit insérer \(x\) à la position correcte dans le sous-tableau trié \(T[1..i-1]\). La boucle interne « tant que » déplace les éléments plus grands que \(x\) vers la droite, et \(j\) décrémente jusqu'à trouver la position correcte pour \(x\). A la fin de la boucle interne, \(T[j]\) est assigné à \(x\). Ainsi, \(T[1..i]\) devient un sous-tableau trié.

Terminaison : La boucle externe « pour » parcourt les indices de \(2\) à \(n\), donc après la dernière itération (\(i = n\)), le tableau complet \(T[1..n]\) est trié.

Variant de boucle⚓︎

Un variant de boucle est une expression qui décroît strictement avec chaque itération de la boucle et est utilisée pour prouver que la boucle se termine.
Pour cet algorithme, on doit identifier deux variants :

Variant de la boucle interne « tant que » :
Un variant pour cette boucle est \(j - 1\). À chaque itération de la boucle interne, \(j\) décrémente de \(1\), donc \(j - 1\) décroît strictement.
Variant de la boucle externe « pour » :
Un variant pour cette boucle est \(n - i\). À chaque itération de la boucle externe, \(i\) augmente de \(1\), donc \(n - i\) décroît strictement.

Terminaison⚓︎

Boucle interne « tant que » :
- Initialisation : au début de la boucle interne, \(j\) est initialisé à \(i\).
- Conservation: à chaque itération, \(j\) est décrémenté de \(1\).
- Borne inférieure : la boucle interne se termine lorsque \(j \le 1\) ou \(x \ge T[j-1]\).
Boucle externe « pour » :
- Initialisation : au début de la boucle externe, \(i\) est initialisé à \(2\).
- ** Conservation** : à chaque itération, \(i\) est incrémenté de \(1\).
- Borne inférieure : La boucle externe se termine lorsque \(i > n\).

Correction⚓︎

Pour prouver la correction de l'algorithme, on doit montrer que pour toute entrée valide (un tableau \(T\) de longueur \(n\)), l'algorithme renvoie le tableau trié.

Invariant de boucle : à chaque début d'itération de la boucle externe, le sous-tableau \(T[1..i-1]\) est trié.

Preuve de terminaison : les variants \(j - 1\) pour la boucle interne et \(n - i\) pour la boucle externe assurent que les deux boucles se terminent.

Post-condition : à la fin de l'algorithme, lorsque \(i = n + 1\), le tableau complet \(T[1..n]\) est trié.

Conclusion⚓︎

En utilisant l'invariant de boucle et les variants, on a prouvé la correction de l'algorithme de tri par insertion.

L'invariant montre que, tout au long de l'exécution, les sous-tableaux partiels sont triés.

Les variants assurent que les boucles se terminent.

Par conséquent, l'algorithme trie correctement le tableau \(T\) et se termine pour toute entrée valide.

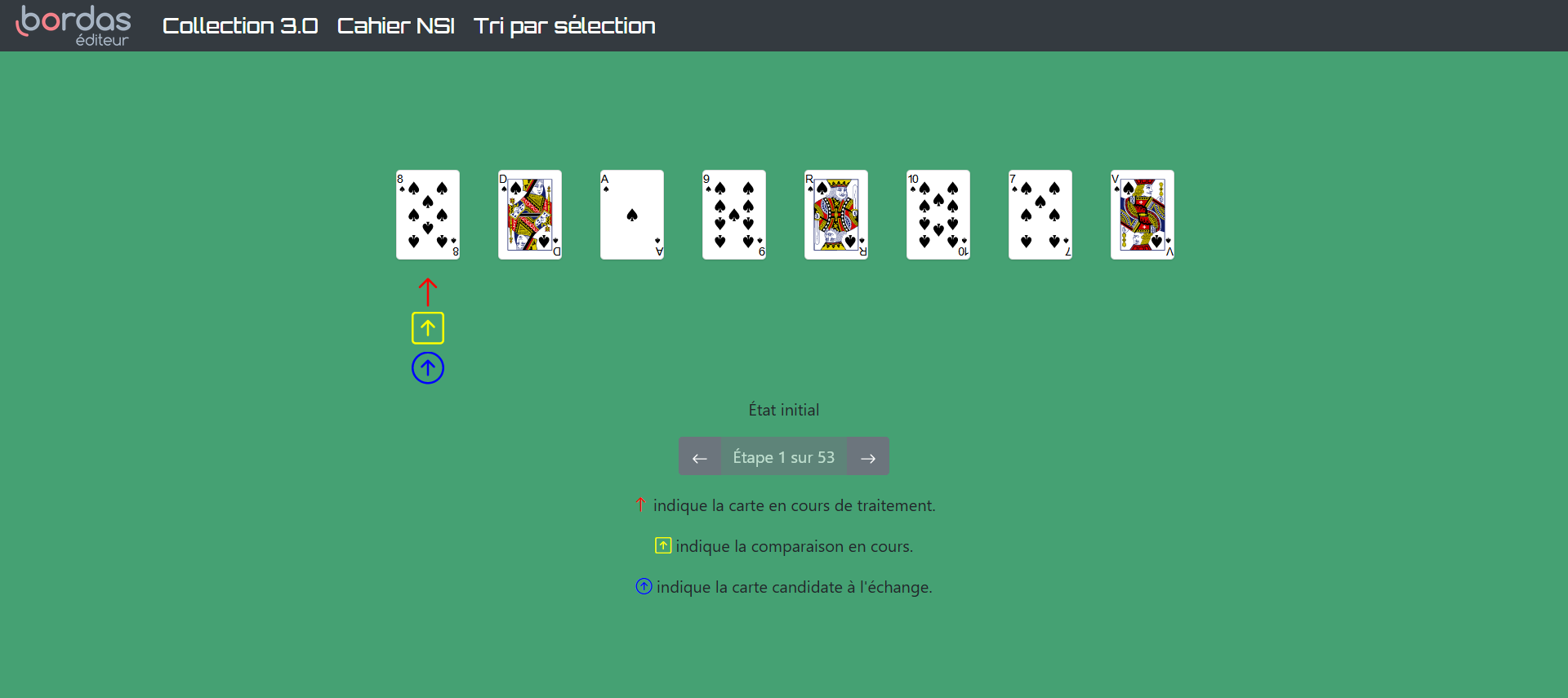
Le tri par sélection⚓︎

Principe⚓︎

On peut traduire l’algorithme de tri par sélection de la façon suivante :

Rechercher le plus petit élément du tableau, et l'échanger avec le 1er élément ;
Rechercher le second plus petit élément du tableau, et l'échanger avec 2ème élément ;
Continuer de cette façon jusqu'à ce que le tableau soit entièrement trié.

Algorithme en pseudocode⚓︎

Pseudocode

// En pseudocode, les indices d'un tableau T vont de 1 à n
pour i de 1 à n-1 faire
    ind_min ← i
    pour j de i+1 à n faire
        si T[j] < T[ind_min] alors
            ind_min ← j
        fin si
    fin pour
    // échange T[i] et T[ind_min]
    temp ← T[i]
    T[i] ← T[ind_min] 
    T[ind_min] ← temp
fin pour

Efficacité de l’algorithme⚓︎

Pour pouvoir comparer avec l’algorithme de tri par insertion, on ne va étudier ici que le nombre de comparaisons du tri par sélection.
On constate que pour le tableau de taille \(5\) à trier par sélection, il y a \(4 + 3 + 2 + 1 = 10\) comparaisons.
Ainsi, pour une taille de tableau donnée, il y a toujours le même nombre de comparaisons, il n’y a donc pas de pire ou meilleur cas (tous les tableaux sont des pires cas). Cela vient du fait que l’on connaît toujours à l’avance le nombre de tours de boucle puisqu’il s’agit de deux boucles pour.

Plus précisément, pour un tableau de taille \(n\) :

Au 1er passage dans la boucle (\(i = 1\)), il y a \(n-1\) comparaisons dans la recherche du plus petit élément ;
Au 2ème passage (\(i = 2\)), il y a \(n-2\) comparaisons ;
Ainsi de suite ... ;
Au dernier passage (\(i = n-1\)), il n’y a plus que \(1\) comparaison (les deux dernières cases).

Il y a donc en tout \((n-1) + (n-2) + ... + 2 + 1 =\dfrac{n(n-1)}{2}\) comparaisons à faire dans le pire cas (dans tous les cas !).
On retrouve donc aussi un coût de l’ordre de \(n^2\) (puisque \(\dfrac{n(n-1)}{2}= \dfrac{n^2}{2}-\dfrac{n}{2}\)).

Complexité temporelle⚓︎

Complexité du tri par sélection

Le tri par sélection a également un coût quadratique dans le pire cas, c’est-à-dire de l’ordre de \(n^2\) (où \(n\) est la taille du tableau).
On dit aussi que sa complexité temporelle est en \(O(n^2)\).
Donc, si on multiplie par \(k\) la taille du tableau, alors le temps de calcul pour faire le tri est multiplié par \(k^2\).
Contrairement au tri par insertion, il y a dans tous les cas \(\dfrac{n(n-1)}{2}\) comparaisons à faire, quel que soit le tableau de départ.

Invariant de boucle⚓︎

Un invariant de boucle est une propriété qui reste vraie avant et après chaque itération de la boucle. Pour cet algorithme, l'invariant de boucle peut être formulé comme suit :

Invariant : à chaque début d'itération de la boucle externe pour \(i\) de \(1\) à \(n-1\), le sous-tableau \(T[1..i-1]\) contient les \(i-1\) plus petits éléments du tableau \(T\) et ils sont triés.

Preuve de l'invariant de boucle :

Initialisation : avant la première itération (\(i = 1\)), le sous-tableau \(T[1..0]\) est vide, ce qui est trivialement trié.

Conservation : supposons que l'invariant est vrai au début de l'itération pour un certain \(i\). Durant l'itération \(i\), l'algorithme cherche l'élément minimum dans le sous-tableau \(T[i..n]\) et le place à la position \(i\) par un échange. Après l'échange, le sous-tableau \(T[1..i]\) contient les i plus petits éléments du tableau et ils sont triés. Ainsi, l'invariant est maintenu pour l'itération suivante.

Terminaison : la boucle externe pour parcourt les indices de \(1\) à \(n-1\), donc après la dernière itération (\(i = n-1\)), le tableau complet \(T[1..n]\) est trié.

Variant de boucle⚓︎

Un variant de boucle est une expression qui décroît strictement avec chaque itération de la boucle et est utilisée pour prouver que la boucle se termine. Pour cet algorithme, on doit identifier deux variants :

Variant de la boucle interne « pour » : Un variant pour cette boucle est \(n - j\).
A chaque itération de la boucle interne, \(j\) augmente de \(1\), donc \(n - j\) décroît strictement.
Variant de la boucle externe « pour »: Un variant pour cette boucle est \(n - i\).
A chaque itération de la boucle externe, \(i\) augmente de \(1\), donc \(n - i\) décroît strictement.

Terminaison⚓︎

Boucle interne « pour » :
- Initialisation : au début de la boucle interne, \(j\) est initialisé à \(i+1\).
- Conservation : à chaque itération, \(j\) est incrémenté de \(1\).
- Borne inférieure : La boucle interne se termine lorsque \(j > n\).
Boucle externe « pour » :
- Initialisation : au début de la boucle externe, \(i\) est initialisé à \(1\).
- Maintien: à chaque itération, \(i\) est incrémenté de \(1\).
- Borne inférieure : la boucle externe se termine lorsque \(i >= n\).

Correction⚓︎

Pour prouver la correction de l'algorithme, on doit montrer que pour toute entrée valide (un tableau \(T\) de longueur \(n\)), l'algorithme renvoie le tableau trié.

Invariant de boucle : à chaque début d'itération de la boucle externe, le sous-tableau \(T[1..i-1]\) est trié et contient les \(i-1\) plus petits éléments du tableau.

**Preuve de Terminaison : les variants \(n - j\) pour la boucle interne et \(n - i\) pour la boucle externe assurent que les deux boucles se terminent.

Post-condition : à la fin de l'algorithme, lorsque \(i = n\), le tableau complet \(T[1..n]\) est trié.

Conclusion⚓︎

En utilisant l'invariant de boucle et les variants, nous avons prouvé la correction de l'algorithme de tri par sélection.

L'invariant montre que, tout au long de l'exécution, les sous-tableaux partiels sont triés et contiennent les plus petits éléments dans l'ordre correct.

Les variants assurent que les boucles se terminent.

Par conséquent, l'algorithme trie correctement le tableau \(T\) et se termine pour toute entrée valide.

Tri par sélection (animation Bordas)