Algorithmes particuliers

Recherche dichotomique⚓︎

Objectif

La recherche dichotomique, ou recherche par dichotomie (en anglais : binary search), est un algorithme de recherche :

pour savoir si un élément est dans un tableau trié ou
pour trouver sa position dans le tableau.

Principe

Comparer l'élément avec la valeur de la case au milieu du tableau :

si les valeurs sont égales, la tâche est accomplie,
sinon on recommence dans la moitié du tableau pertinente.

Algorithme

Pseudocode

// En pseudocode les indices des éléments du tableau T varient de 1 à n
debut ← 1
fin ← taille de T

tant que debut ≤ fin :
    milieu ← (debut + fin)/2
    val_milieu ← T[milieu]
    si val = val_milieu :
        renvoyer Vrai
    si val < val_milieu :
        fin ← milieu - 1
    si val > val_milieu :
        debut ← milieu + 1
renvoyer Faux

Vidéo de Cédric Gerland (15:33)

Fichier PDF (Eduscol)

Algorithme des k plus proches voisins⚓︎

Vidéo de Cédric Gerland (12:47)

Fichier PDF (Eduscol)

Algorithmes gloutons⚓︎

Objectifs

Comprendre la notion d’algorithme glouton
Résoudre un problème grâce à un algorithme glouton.

Principe

Un algorithme glouton (en anglais : « greedy ») est un algorithme qui suit le principe de faire, étape par étape, un choix optimum local, dans l'espoir d'obtenir un résultat optimum global.
Cet algorithme permet d’obtenir rapidement un résultat global, mais n’assure pas que ce résultat soit optimal.

Optimisation d’un problème

Optimiser un problème, c’est déterminer les conditions dans lesquelles ce problème présente une caractéristique spécifique. Par exemple, dans le domaine des mathématiques, déterminer le minimum ou le maximum d’une fonction est un problème d’optimisation.
De nombreuses situations relèvent d’un problème d’optimisation :

recherche du plus court chemin entre deux points géographiques par un GPS
rendu de monnaie par un distributeur de boisson
chargement d’un sac à dos …
etc ...

De nombreuses techniques informatiques sont susceptibles d’apporter une solution exacte ou approchée à ces problèmes. Certaines de ces techniques, comme l’énumération exhaustive de toutes les solutions, ont un coût machine qui les rend souvent peu pertinentes au regard de contraintes extérieures imposées (temps de réponse de la solution imposé, moyens machines limités).

Intérêt et limites des algorithmes gloutons

Les algorithmes gloutons constituent une méthode possible de résolution de ce type de problème.
Cependant, le résultat auquel ils conduisent n’est pas toujours la solution optimale : il s’agit souvent d’un optimum possible mais pas de l’optimum. Plus précisément, ces algorithmes déterminent un optimum en effectuant successivement des choix locaux, jamais remis en cause.
Au cours de la construction de la solution, l’algorithme résout une partie du problème puis se focalise ensuite sur le sous-problème restant à résoudre. Le principal avantage des algorithmes gloutons est leur facilité de mise en oeuvre.

Une différence essentielle avec la programmation dynamique (cours de terminale), plus efficace mais plus compliquée à implémenter, est que celle-ci peut remettre en cause des solutions déjà établies. Au lieu de se focaliser sur un seul sous-problème, elle explore les solutions de tous les sous-problèmes pour les combiner finalement de manière optimale.

Problème de rendu de monnaie⚓︎

Enoncé du problème

Comment rendre une somme de $17$ € avec le moins de pièces et billets possible, parmi les pièces $10$, $5$, $2$ et $1$ € ?

Algorithme

On rend la monnaie en commençant toujours la pièce ou le billet de valeur maximale (tant qu’on ne dépasse pas la somme à rendre) puis en continuant par valeurs décroissantes.

PseudocodePython

Pseudocode

\\ Algorithme glouton de rendu de monnaie (modèle LARP)

DÉBUT
    \\ système monétaire volontairement simplifié
    monnaie = [1, 2 , 5, 10]
    \\ indices des éléments du tableau monnaie vont de 1 à 4 
    ÉCRIRE "Somme à rendre ? "
    LIRE somme
    rendu = []
    a_rendre = somme
    \\ nombre de pièces ou billets
    i = CAPACITÉ(monnaie)
    TANTQUE a_rendre > 0 ET i ≥ 1 FAIRE
        SI a_rendre ≥ monnaie[i] ALORS
            a_rendre = a_rendre - monnaie[i]
            rendu = rendu + [monnaie[i]]
        SINON
            i = i-1
        FINSI
    FINTANTQUE
    ÉCRIRE rendu
FIN

🐍 Editeur

# Algorithme glouton de rendu de monnaie

# système monétaire volontairement simplifié
monnaie = [1, 2 , 5, 10]
somme = int(input("Somme à rendre ? "))
rendu = []
a_rendre = somme
# nombre de pièces ou billets
i = len(monnaie)-1
while a_rendre > 0 and i >= 0:
    if a_rendre >= monnaie[i]:
        a_rendre = a_rendre - monnaie[i]
        rendu = rendu + [monnaie[i]]
    else:
        i = i-1
print(rendu)

▶️ Console

>>>
Somme à rendre ? 17
[10, 5, 2]

Conclusion

Cet algorithme glouton est la méthode employée en pratique, car il renvoie la solution optimale avec les systèmes de monnaie généralement utilisés dans le monde. Ces systèmes sont dits « canoniques ». Le système de l’euro est canonique.
Pour rendre $6$ €, on rend un billet de $5$ € et une pièce de $1$ €.
Avec un système de monnaie non canonique [$1$, $3$, $4$], pour rendre $6$, l’algorithme glouton rend $4$, puis $1$, puis $1$, soit trois pièces, alors que la solution optimale serait de rendre deux pièces de $3$.

Fichier PDF (Eduscol)

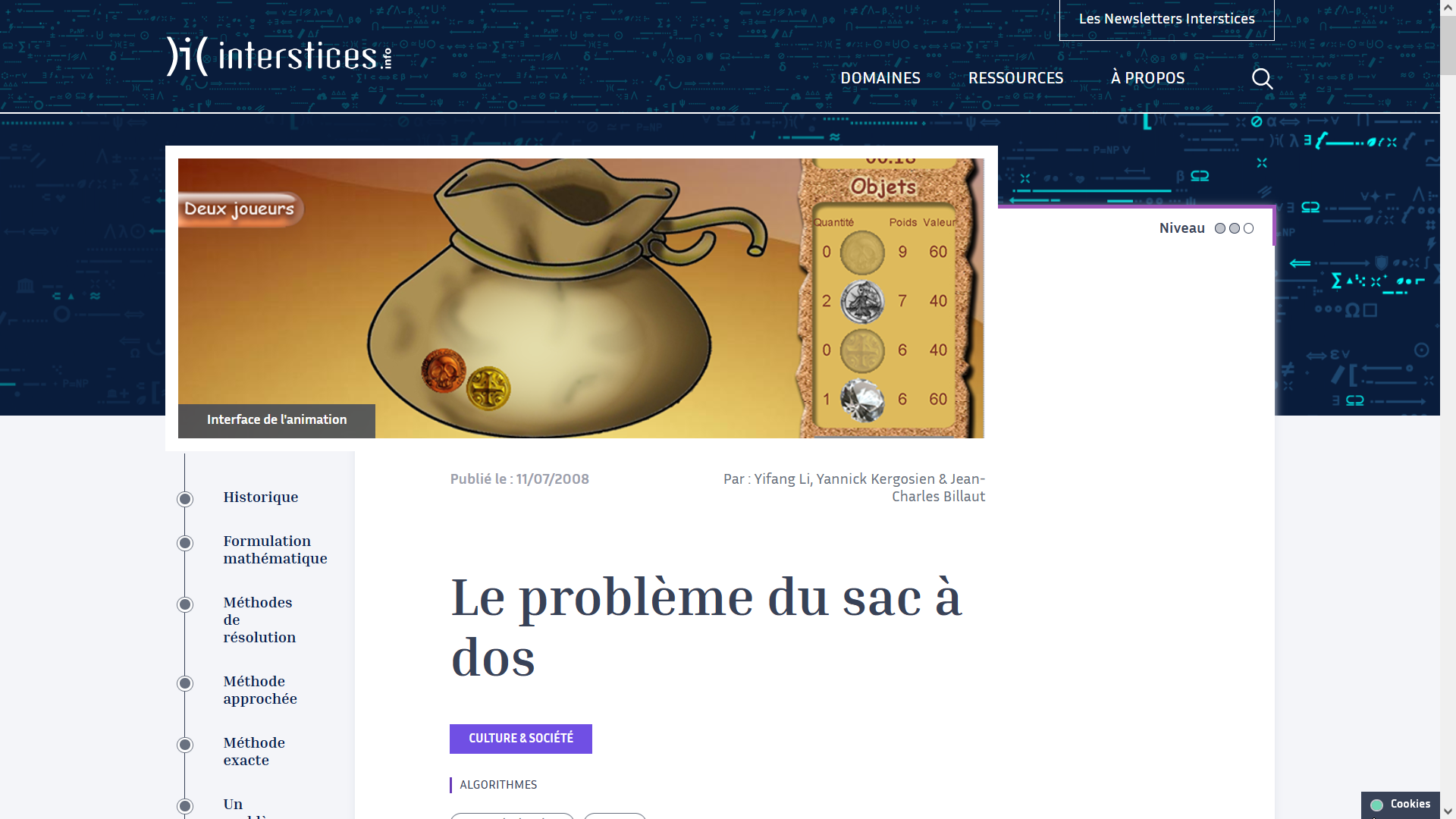
Problème du sac-à-dos⚓︎

Historique

En algorithmique, le problème du sac à dos, noté également KP (en anglais, Knapsack problem) est un problème d'optimisation combinatoire. Il modélise le remplissage d'un sac à dos, ne pouvant supporter plus d'une certaine masse, avec tout ou partie d'un ensemble donné d'objets ayant chacun une valeur spécifique en euros. Les objets mis dans le sac à dos doivent maximiser la valeur totale en euros, sans dépasser la masse maximale.

Le problème du sac à dos est l'un des 21 problèmes NP-complets du mathématicien américain Richard Karp, exposés dans son article de 1972. Ce dernier reçu le prix Turing en 1985 pour ses travaux.

On retrouve aussi ce type de problème sous d'autres formes :

dans la finance: étant donné un certain montant d’investissement dans des projets, quels projets choisir pour que le tout rapporte le plus d’argent possible;
pour la découpe de matériaux, afin de minimiser les pertes dues aux chutes;
dans le chargement de cargaisons (avions, camions, bateaux, ...).
etc ...

Enoncé du problème du sac à dos

Parmi les objets proposés lesquels choisir afin de maximiser la valeur totale emportée tout en ne dépassant pas la masse maximale $M$ autorisée du sac-à-dos ?

Mise en équation mathématique du problème

Le sac-à-dos de masse maximale $M$ kg et on dispose d'une collection de $n$ objets ($n \in \mathrm{N^*}$). Pour chaque objet $i$, nous avons une masse $m_i$ et une valeur $v_i$. On définit la variable $x_i$ associée à un objet $i$ de la façon suivante :

$x_i = 1$ si l’objet $i$ est mis dans le sac, et
$x_i = 0$ si l’objet $i$ n’est pas mis dans le sac.
Objectif 1 : respecter la contrainte de la masse totale : $\sum\limits_{i=0}^n~x_i \times m_i \leqslant M$
Objectif 2 : maximiser la valeur totale des objets : $max \left(\sum\limits_{i=0}^n~x_i \times v_i \right)$

Sac à dos : méthode naïve (ou exhaustive)

Considérons les objets suivants et un sac de capacité maximale $M = 15~kg$ :

Objet n° $i$	$1$	$2$	$3$	$4$	$5$	$6$
masse $m_i$ (kg)	14	2	5	1	6	8
valeur $v_i$ (€)	126	32	20	5	18	80

Une première méthode consiste à :

lister toutes les combinaisons possibles d'objets puis
regarder lesquelles ne dépassent pas la masse maximals admissible $M$ du sac-à-dos et enfin
regarder laquelle permet d'avoir une somme maximale.

Combien y a-t-il alors de combinaisons possibles ?

En considérant chaque objet, on peut :

soit le prendre,
soit le laisser.

Il y a donc 2 choix possibles.

Soit avec $6$ objets, $2^6 = 64$ combinaisons à examiner, ce qui reste raisonnable.
Soit avec $50$ objets, $2^{50} = 1~125~899~906~842~624$ combinaisons, ce qui est plus ardu.

Conclusion : Le coût de la méthode naïve est donc en $O(2^n)$, c'est un coût exponentiel.

Sac à dos : algorithme glouton

Considérons les objets suivants et un sac de capacité maximale $M = 15~kg$ :

Objet n° $i$	$1$	$2$	$3$	$4$	$5$	$6$
masse $m_i$ (kg)	14	2	5	1	6	8
valeur $v_i$ (€)	126	32	20	5	18	80
ratio $r_i = v_i/m_i$	9	16	4	5	3	10

On rappelle qu'il y a plusieurs stratégies gloutonnes pour trouver une solution du problème :

Stratégie 1 : choix des objets par masses $m_i$ croissantes.
On obtient avec les objets $4$, $2$, $3$ et $5$ :
$m_{sac} = m_4 + m_2 + m_3 + m_5 = 1 + 2 + 5 + 6 = 14~kg \leq M = 15~kg$
$v_{sac} = v_4 + v_2 + v_3 + v_5 = 5 + 32 + 20 + 18 = 75~\textit{€}$

Stratégie 2 : choix des objets par valeurs $v_i$ décroissantes.
On obtient avec les objets $1$, et $4$ seul :
$m = m_1 + m_4 = 14 + 1 = 15~kg \leq M = 15~kg$
$v = v_1 + v_4 = 126 + 5 = 129~\textit{€} $

Stratégie 3 : choix des objets par ratios $r_i$ décroissants.
On obtient avec les objets $2$, $6$ et $4$ :
$m_{sac} = m_2 + m_6 + m_4 = 2 + 8 + 1 = 11~kg \leq M = 15~kg$
$v_{sac} = v_2 + v_6 + v_4 = 32 + 80 + 5 = 117~\textit{€}$

Conclusion : le résultat obtenu ici en appliquant l'algorithme glouton est meilleur si l'on raisonne sur les valeurs $v_i$ (stratégie n° 2) plutôt que sur les masses $m_i$ ou les ratios valeur/masse $v_i/m_i$ des différents objets.

Remarque : La solution optimale est obtenue,en réalité, en prenant les objets $2$, $3$ et $6$ :

$m_{sac} = m_2 + m_3 + m_6 = 2 + 5 + 8 = 15~kg \leq M = 15~kg$
$v_{sac} = v_2 + v_3 + v_6 = 32 + 20 + 80 = 132~\textit{€}$

Site interstices.info

Fichier PDF (Eduscol)

Algorithmes animés⚓︎

Site de Fred Boissac site non sécurisé

Objet n° \(i\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
masse \(m_i\) (kg)	14	2	5	1	6	8
valeur \(v_i\) (€)	126	32	20	5	18	80

Objet n° \(i\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
masse \(m_i\) (kg)	14	2	5	1	6	8
valeur \(v_i\) (€)	126	32	20	5	18	80
ratio \(r_i = v_i/m_i\)	9	16	4	5	3	10