Logique booléenne
Transistors NPN et PNP en commutation (simulation)⚓︎
Application Lushprojects en ligne
Portes logiques de base⚓︎
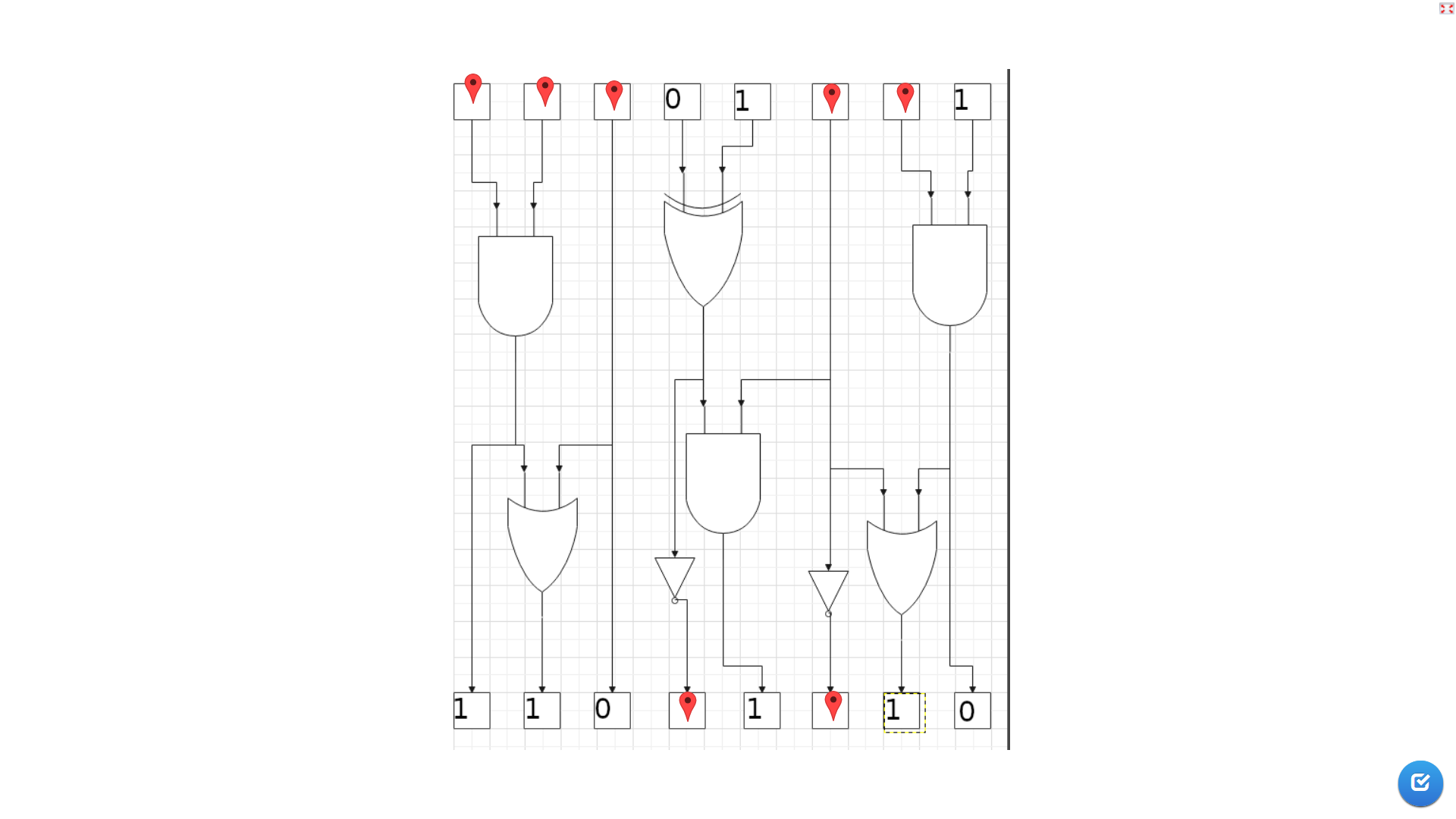
Simulateur de modulo-info.ch⚓︎
Application en ligne
Simulateur SimcirJS⚓︎
Application en ligne
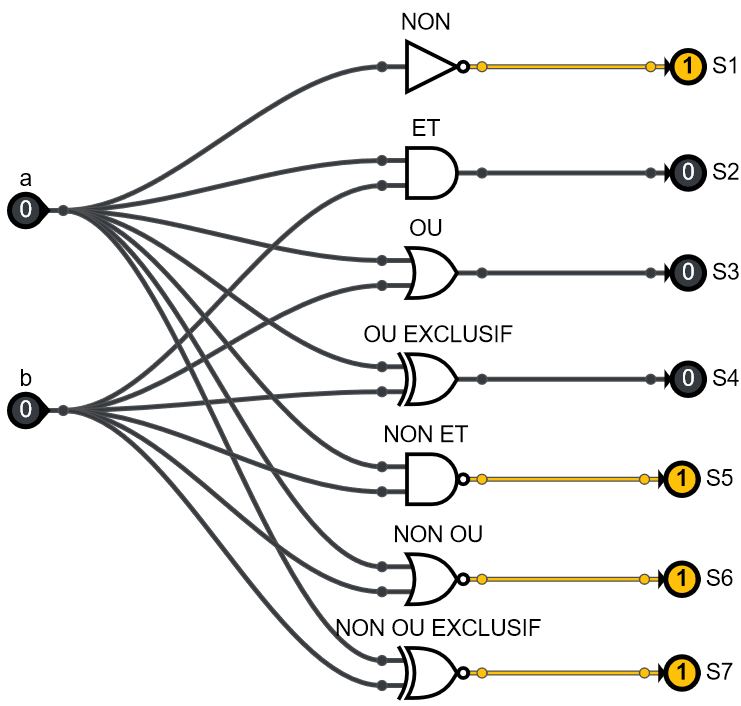
Tables de vérité des fonctions booléennes de base⚓︎
Tables de vérité des cellules logiques NON, ET, OU, NON-ET, NON-OU, OU-EXCLUSIF
| Entrée 1 | Entrée 2 | NON | NON | ET | OU |
|---|---|---|---|---|---|
| \(a\) | \(b\) | \(\overline{a}\) | \(\overline{b}\) | \(a.b\) | \(a+b\) |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| Entrée 1 | Entrée 2 | NON-ET | NON-OU | OU-EXCLUSIF |
|---|---|---|---|---|
| \(a\) | \(b\) | \(\overline{a.b}\) | \(\overline{a+b}\) | \(\overline{a}.b+a.\overline{b}\) = \(a\oplus b\) |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
Logique combinatoire ou logique séquentielle⚓︎
Logique combinatoire et logique séquentielle
La logique combinatoire et la logique séquentielle sont deux types fondamentaux de circuits utilisés en électronique numérique, chacun ayant des caractéristiques et des comportements distincts.
Logique combinatoire
Définition : Un circuit de logique combinatoire est un type de circuit où la sortie dépend uniquement des entrées actuelles. Il n’y a pas de mémoire ou d’éléments de stockage des états précédents.
Comportement : Chaque combinaison d'entrées produit une sortie fixe, selon une fonction logique déterminée (comme des portes logiques telles que AND, OR, XOR, etc.).
Exemples : Les additionneurs, les multiplexeurs, les décodeurs et les portes logiques élémentaires (AND, OR, NOT, etc.).
Caractéristiques :
- Ne stocke pas d’informations, pas de notion de temps.
- La sortie change instantanément (ou avec un petit délai de propagation) dès que les entrées changent.
- Fonction purement déterministe et sans mémoire.
Schéma de fonctionnement :
flowchart LR
A[Entrées] -->|Fonction logique| B[Sorties]Logique séquentielle
Définition : Un circuit de logique séquentielle est un circuit dont la sortie dépend non seulement des entrées actuelles mais aussi de l’état précédent du système. Cela signifie qu’il y a des éléments de mémoire ou des boucles de rétroaction qui stockent l’état.
Comportement : Ce type de circuit utilise des dispositifs comme des bascules (flip-flops) ou des registres pour mémoriser l’état. Le système évolue en fonction des entrées et de l’état précédent, ce qui introduit une notion de temps et de séquence.
Exemples : compteurs, registres, bascules (flip-flops), machines d'état finies (FSM).
Caractéristiques :
- Stocke des informations sous forme d’états internes.
- La sortie dépend des états passés (mémoire) et des entrées actuelles.
- Utilise un signal d'horloge pour coordonner les changements d'état.
Schéma de fonctionnement :
flowchart LR
A[Entrées + Etats passés] -->|Horloge| B[Sorties + Nouveaux états]Principales différences
| Aspect | Logique combinatoire | Logique séquentielle |
|---|---|---|
| Dépendance | Dépend uniquement des entrées actuelles | Dépend uniquement des entrées actuelles et de l'état précédent |
| Mémoire | Aucune mémoire (sans état) | Utilise la mémoire (avec état) |
| Signal d'horloge | Pas d'horloge | Utilise souvent une horloge |
| Exemples | Additionneur, multiplexeur, portes logiques | Compteur, registre, bascule |
| Utilisation | Opérations purement combinatoires | Opérations nécessitant une séquence temporelle |
Conclusion : La logique combinatoire se concentre sur des opérations immédiates et sans mémoire, tandis que la logique séquentielle gère des processus qui dépendent du temps et nécessitent une mémoire pour suivre l’évolution de l'état du circuit.
Exemple : bascule D synchrone et équivalent
Logique booléenne en Python⚓︎
Exemples en Python
# Tests (insensible à la casse)(Ctrl+I)
# Tests (insensible à la casse)(Ctrl+I)
# Tests (insensible à la casse)(Ctrl+I)
Tests sur la logique booléenne (LearningApps.org)⚓︎
Test n°1 - Logique binaire
Test n°2 - Logique binaire
Test n°3 - Table de vérité des fonctions logiques de base
Test n°4 - Remplir une table de vérité
Test n°5 - Schéma logique
Séquentialité des opérateurs booléens et évaluation paresseuse (Python)⚓︎
Caractère séquentiel des opérateurs booléens (Python)⚓︎
En Python, les opérateurs logiques sont utilisés pour combiner des expressions booléennes (vraies ou fausses). Les opérateurs logiques principaux sont and, or, et not. L'évaluation de ces opérateurs peut être influencée par deux concepts importants : l'aspect séquentiel et l'évaluation paresseuse.
Aspect séquentiel des opérateurs logiques
En Python, les expressions sont évaluées de gauche à droite. L'ordre d'évaluation est important car les opérateurs logiques peuvent court-circuiter (stopper l'évaluation) dès que le résultat de l'expression est déterminé.
Opérateur and
Pour l'opérateur and, si la première expression est False, Python n'évaluera pas la deuxième expression car le résultat de and sera forcément False.
Exemple :
a = False
b = True
# Ici, `b` ne sera jamais évalué car `a` est False
resultat = a and b
print(resultat) # Output: False
a d'abord. Puisque a est False, Python sait que a and b sera False quel que soit le résultat de b, donc il n'évalue même pas b.
Opérateur or
Pour l'opérateur or, si la première expression est True, Python n'évaluera pas la deuxième expression car le résultat de or sera forcément True.
Exemple :
a = True
b = False
# Ici, `b` ne sera jamais évalué car `a` est True
resultat = a or b
print(resultat) # Output: True
Dans cet exemple, Python évalue a d'abord. Puisque a est True, Python sait que a or b sera True quel que soit le résultat de b, donc il n'évalue même pas b.
Evaluation paresseuse (Python)⚓︎
Évaluation paresseuse (short-circuit evaluation)
L'évaluation paresseuse est une optimisation que Python utilise pour éviter des calculs inutiles. Cela se produit avec and et or comme vu précédemment.
Exemple d'évaluation paresseuse avec and
def retourne_false():
print("Fonction retourne_false appelée")
return False
def retourne_true():
print("Fonction retourne_true appelée")
return True
resultat = retourne_false() and retourne_true()
print(resultat)
retourne_false() est appelé en premier. Comme il retourne False, Python ne va pas exécuter retourne_true() car cela ne changerait pas le résultat final.
Exemple d'évaluation paresseuse avec or
def retourne_false():
print("Fonction retourne_false appelée")
return False
def retourne_true():
print("Fonction retourne_true appelée")
return True
resultat = retourne_true() or retourne_false()
print(resultat)
Ici, retourne_true() est appelé en premier. Puisqu'il retourne True, Python n'appelle pas retourne_false() car cela ne changerait pas le résultat final.
Utilisation pratique de l'évaluation paresseuse
L'évaluation paresseuse est particulièrement utile dans les situations où l'évaluation complète de toutes les conditions n'est pas nécessaire ou pourrait entraîner une erreur. Par exemple, vérifier si une variable n'est pas None avant d'accéder à ses méthodes ou propriétés :
objet = None
# On vérifie d'abord si `objet` n'est pas None avant d'appeler une méthode
if objet is not None and objet.methode():
print("Méthode appelée avec succès")
else:
print("Objet est None ou méthode a échoué")
Dans ce code, Python ne tentera pas d'appeler objet.methode() si objet est None, évitant ainsi une potentielle exception AttributeError.
Conclusion⚓︎
L'aspect séquentiel des opérateurs logiques et l'évaluation paresseuse sont des concepts fondamentaux en Python qui permettent d'optimiser le code et d'éviter des erreurs potentielles. Comprendre comment et quand Python évalue les expressions est crucial pour écrire du code efficace et robuste.
# Tests(insensible à la casse)(Ctrl+I)