Arbres

Arbre et définitions⚓︎

Arbre et définitions

En informatique, un « arbre » est une structure de données hiérarchique composée de noeuds interconnectés par des arêtes ou branches. Chaque noeud de l'arbre peut avoir un noeud parent, des noeuds enfants et des noeuds frères. La structure de l'arbre commence par un noeud racine, qui est le noeud le plus haut de l'arbre.

%%{
  init: {
    'theme': 'base',
    'themeVariables': {
    }
  }
}%%
graph TD;
Racine --> Feuille1;
Racine --> Noeud1;
Noeud1 --> Noeud2;
Noeud1 --> Feuille2;
Noeud1 --> Feuille3;
Noeud2 --> Feuille4;

classDef root1 fill:#D0E1F9,stroke:#6699CC,stroke-width:2px;
classDef node fill:#F7E1A0,stroke:#CC9900,stroke-width:2px;
classDef leaf fill:#D0E8D0,stroke:#66CC66,stroke-width:2px;

class Racine root1;
class Noeud1,Noeud2 node;
class Feuille1,Feuille2,Feuille3,Feuille4 leaf;

Voici une définition simple d'un arbre en informatique :

Un arbre est une structure de données non linéaire composée de noeuds interconnectés par des branches.
Un arbre a une structure hiérarchique, avec chaque noeud ayant un noeud parent (sauf pour le noeud racine), des noeuds enfants et des noeuds frères.
Le noeud racine est le noeud le plus haut de l'arbre, et il n'a pas de noeud parent.
Chaque noeud de l'arbre peut avoir zéro ou plusieurs noeuds enfants, mais chaque noeud enfant peut avoir seulement un noeud parent.
Les noeuds en bas de l'arbre, qui n'ont pas de noeuds enfants, sont appelés noeuds feuilles ou noeuds terminaux.
La profondeur d'un noeud est le nombre d'arêtes du noeud racine à ce noeud.
La hauteur d'un arbre est la profondeur maximale de n'importe quel noeud de l'arbre.

Les arbres sont couramment utilisés en informatique pour représenter des données hiérarchiques, telles que les systèmes de fichiers, les structures de répertoires et les organigrammes. Ils sont également utilisés dans les algorithmes de recherche et de tri de données, et dans les structures de données telles que les arbres de recherche binaires et les tas.

Arbres binaires⚓︎

Les arbres binaires sont des arbres de degré inférieur ou égal à 2. Chaque noeud a au plus deux fils :

graph TD
    gp[...]
    pg[père]
    pd[...]
    fg[fils gauche]
    fd[fils droit]
    pfgg[...]
    pfgd[...]
    pfdg[...]
    pfdd[...]
    gp:::hidden --- pg
    gp ~~~ pd:::hidden
    pg --- fg
    pg --- fd
    fg --- pfgg:::hidden
    fg --- pfgd:::hidden
    fd --- pfdg:::hidden
    fd --- pfdd:::hidden

    classDef hidden display: none;

Définitions⚓︎

graph TD;
    subgraph Racine
        A
    end

    subgraph Père
        B
    end
    C

    A --> B
    A --> C

    B --> D[Fils gauche 1]
    B --> E[Fils droit 1]

    C --> F[Fils gauche 2]
    C --> G[Fils droit 2]

    D --> H[Fils gauche 1.1]
    D --> I[Fils droit 1.1]

    E --> J[Fils gauche 1.2]
    E --> K[Fils droit 1.2]

    F --> L[Fils gauche 2.1]
    F --> M[Fils droit 2.1]

    G --> N[Fils gauche 2.2]
    G --> O[Fils droit 2.2]

Exercice sur les définitions associées aux arbres

Travail demandéCorrigé

graph TD
  A((A))
  B((B))
  C((C))
  D((D))
  E((E))
  F((F))
  G((G))
  H((H))
  I((I))
  J((J))
  K((K))
  A --> B & C
  B --> D & E
  C ~~~ Z:::hidden
  C --> F
  D --> G & H
  E ~~~ Y:::hidden
  E --> I
  F --> J
  F --> K

  classDef hidden display: none;

1. Quelle est la racine de cet arbre ?
2. Quels sont les sous-arbres de B ?
3. Quel est le degré de la racine ? De l'arbre ?
4. Quelles sont les feuilles ?
5. Quels sont les descendants de B ?
6. Quels sont les ancêtres de K ?
7. Quels sont les cousins de F ?
8. Quel est l'oncle de G ?
9. Quels sont les noeuds de niveau 3 ?
10. Quelle est la hauteur de l'arbre ?

graph TD
  subgraph racine
    A((A)):::root
  end
  subgraph "père"
  B((B)):::internal
  end
  C((C)):::internal
  subgraph "fils gauche"
    D((D)):::internal
  end
  subgraph "fils droit"
    E((E)):::internal
  end
  F((F)):::internal
  G((G)):::leaf
  H((H)):::leaf
  I((I)):::leaf
  J((J)):::leaf
  K((K)):::leaf
  A --> B & C
  B --> D & E
  C ~~~ Z:::hidden
  C --> F
  D --> G & H
  E ~~~ Y:::hidden
  E --> I
  F --> J
  F --> K

  classDef hidden display: none;
  classDef root fill:#f9f,stroke:#333,stroke-width:1px;
  classDef internal fill:#f96,stroke:#333,stroke-width:1px;
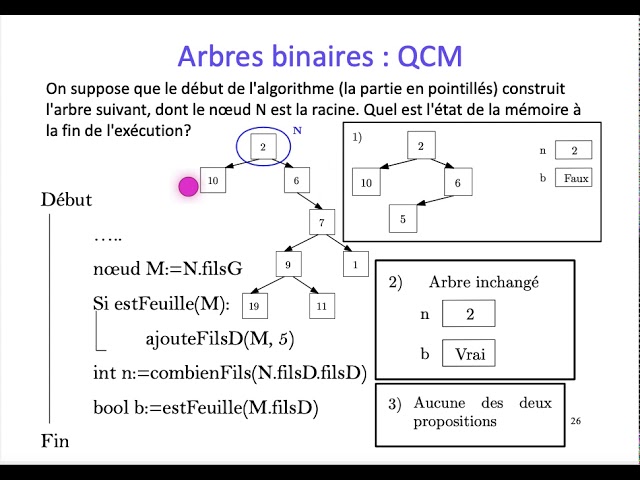
  classDef leaf fill:#6f9,stroke:#333,stroke-width:1px;

1. Racine de cet arbre : noeud A car (point de départ des branches de l'arbre)
2. Sous-arbres de B : les noeuds D et E. Ces deux noeuds sont les fils de B et forment les sous-arbres de B. Sous-arbre gauche de B : D a pour fils G et H Sous-arbre droit de B : E a pour fils I.
3. Degré de la racine A = 2 (car elle a deux enfants directs : B et C)
Degré de l'arbre = 2 (nombre maximum de fils qu'un noeud peut avoir, ici, les noeuds A, B, D et F ont deux fils).
4. Feuilles sont les noeuds qui n'ont pas de descendants, c'est-à-dire les noeuds terminaux de l'arbre.
Les feuilles de cet arbre sont : G, H, I, J, et K.
5. Descendants de B = noeuds qui viennent après B dans l'arbre : D, G, H, E et I.
6. Ancêtres de K = tous les noeuds sur le chemin depuis la racine jusqu'à K : A (racine), C (père de F), F (père de K).
7. Cousins de F = les noeuds qui sont à la même profondeur mais qui ne partagent pas le même père : Les cousins de F sont D et E, car ils sont au même niveau dans l'arbre et n'ont pas le même père que F.
8. Oncle de G = les frères des parents de G. Le père de G est D, donc le frère de D est E. Par conséquent, les oncles de G sont B et D.
9. Noeuds de niveau 3 = ceux qui se trouvent trois niveaux en dessous de la racine : G,L, M, N, O, P. Ce sont les fils de E et H.
10. Hauteur de l'arbre = 4 (nombre de niveaux entre la racine et la feuille la plus éloignée). Ici, la feuille la plus profonde est P, qui se trouve à 4 niveaux (de A à P).