Graphes

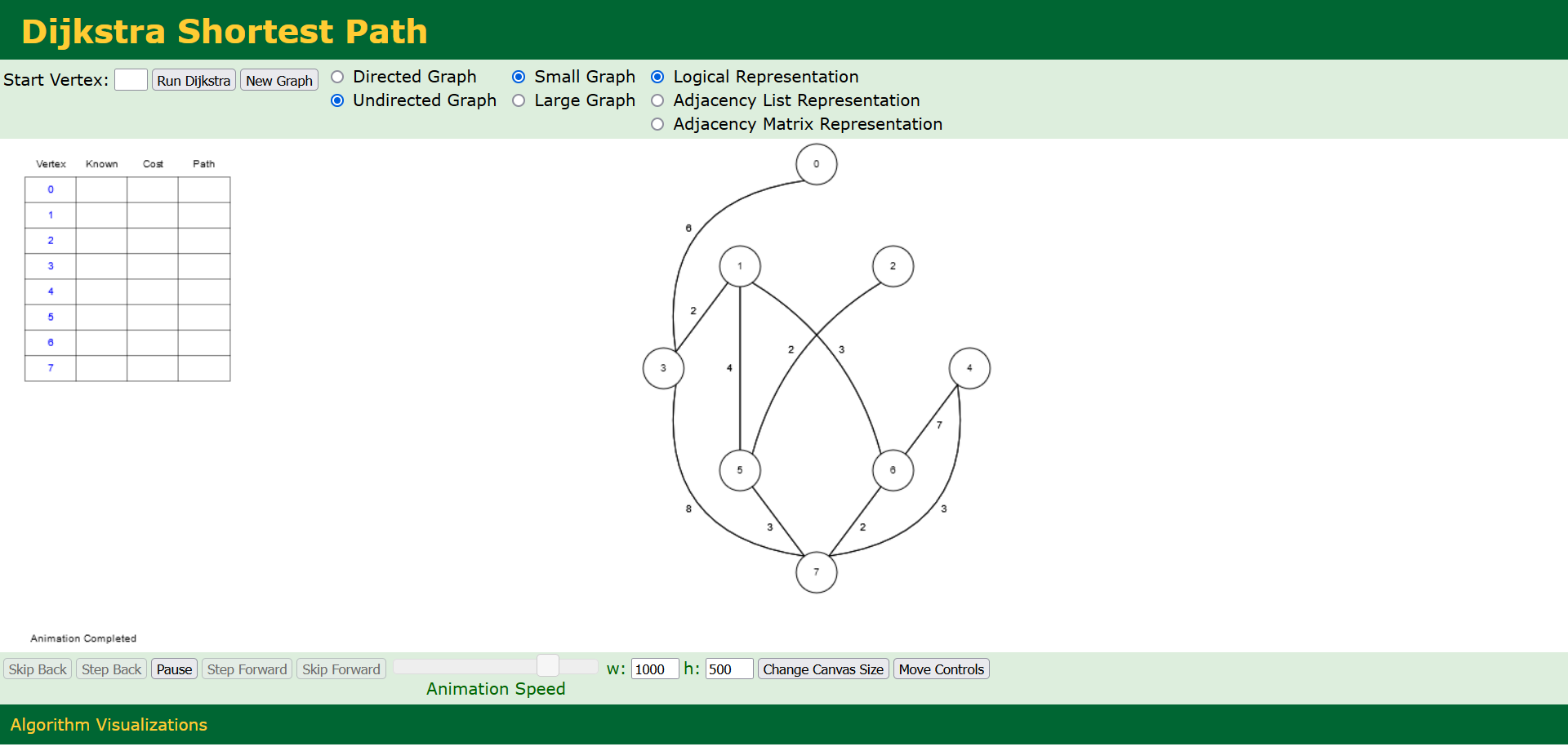
Graphes⚓︎

Graphe coloré Mermaid

graph TD
  A[Noël] -->|Gagner de l'argent| B(Acheter des cadeaux)
  subgraph T ["Test"]
    A
    B
  end
  classDef Test fill:#F84E68,stroke:#333,color:blue;
  class A,T Test
  classDef TestSub fill:wheat;
  class T TestSub
  linkStyle 0 color:blue,stroke:orange;

Graphe non orienté⚓︎

Graphe non orienté horizontal Graphviz

Graphe non orienté Mermaid

graph TB
    A --- B

Graphe non orienté Mermaid

graph TD
  op1(("-")) --- op2(("*")) & op3(("*"))
  op2 --- 3 & x
  op3 --- op4(("-")) & op5(("+"))
  op4 --- 2 & y
  op5 --- 5 & z

Graphe non orienté

Un graphe non orienté est une structure abstraite de données composée d'un ensemble de ressources_infos (ou sommets) et d'un ensemble de liens (ou arêtes) entre ces ressources_infos. Contrairement aux graphes orientés, dans les graphes non orientés, les arêtes n'ont pas de direction, ce qui signifie que la connexion entre deux noeuds est bidirectionnelle.

Composants d'un graphe non orienté :

Noeuds (sommets) : les entités principales du graphe. Par exemple, dans un graphe représentant un réseau social, les noeuds peuvent représenter des personnes.
Arêtes (liens) : les connexions entre les noeuds. Dans un réseau social, une arête pourrait représenter une amitié entre deux personnes.

Représentation en Python :

En Python, les graphes non orientés peuvent être représentés de plusieurs façons, notamment avec des listes d'adjacence ou des matrices d'adjacence. Voici comment les deux représentations peuvent être implémentées :

1. Liste d'adjacence

Une liste d'adjacence utilise un dictionnaire où chaque clé représente un nœud et la valeur associée est une liste des noeuds adjacents.

🐍 Editeur

# Création d'un graphe non orienté avec une liste d'adjacence
graphe = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# Affichage du graphe
for noeud in graphe:
    print(f"{noeud} -> {graphe[noeud]}")

▶️ Console

A -> ['B', 'C']
B -> ['A', 'D', 'E']
C -> ['A', 'F']
D -> ['B']
E -> ['B', 'F']
F -> ['C', 'E']

Dans cet exemple, le graphe est représenté par un dictionnaire. Le nœud 'A' est connecté aux ressources_infos 'B' et 'C', le noeud 'B' est connecté aux ressources_infos 'A', 'D', et 'E', et ainsi de suite.

2. Matrice d'adjacence

Une matrice d'adjacence est une matrice carrée où les lignes et les colonnes représentent les ressources_infos et une cellule contient 1 si une arête existe entre les deux noeuds correspondants, sinon 0.

🐍 Editeur

# ressources_infos du graphe
ressources_infos = ['A', 'B', 'C', 'D', 'E', 'F']

# Matrice d'adjacence du graphe non orienté
matr_adj = [
    [0, 1, 1, 0, 0, 0],  # A
    [1, 0, 0, 1, 1, 0],  # B
    [1, 0, 0, 0, 0, 1],  # C
    [0, 1, 0, 0, 0, 0],  # D
    [0, 1, 0, 0, 0, 1],  # E
    [0, 0, 1, 0, 1, 0]   # F
]

# Affichage de l'entête de la matrice d'adjacence
print(" ", end=" ")
for noeud in ressources_infos:
    print(noeud, end=" ")
print()  # Nouvelle ligne après l'entête

# Affichage de la matrice d'adjacence
for i in range(len(matr_adj)):
    print(ressources_infos[i], end=" ")
    for valeur in matr_adj[i]:
        print(valeur, end=" ")
    print()  # Nouvelle ligne après chaque rangée

▶️ Console

  A B C D E F 
A 0 1 1 0 0 0 
B 1 0 0 1 1 0 
C 1 0 0 0 0 1 
D 0 1 0 0 0 0 
E 0 1 0 0 0 1 
F 0 0 1 0 1 0

Dans cet exemple, la matrice d'adjacence indique que le noeud 'A' est connecté aux ressources_infos 'B' et 'C' (car mat_adj[0][1] et mat_adj[0][2] sont tous les deux égaux à 1).

Conclusion :

Les graphes non orientés sont très utiles dans divers domaines tels que les réseaux sociaux, la modélisation de relations, les réseaux de transport, etc. Python offre des structures de données flexibles pour représenter et manipuler ces graphes, facilitant ainsi leur utilisation dans des applications réelles.

Graphe orienté⚓︎

Graphe orienté Graphviz : Earth -> Mars

Graphe orienté Graphviz

Graphe orienté horizontal Graphviz

Graphe orienté avec sommet masqué et lien masqué Mermaid

flowchart LR
  box1 --> box2
  box2 --- box3:::hidden
  box4 ~~~ box2

Graphe orienté

Les graphes orientés sont une structure de données composée d'un ensemble de noeuds (ou sommets) reliés entre eux par des arcs orientés (ou arêtes) qui ont une direction. Dans un graphe orienté, chaque arête a une direction associée qui va d'un sommet à un autre. Cela signifie que si une arête relie le sommet A au sommet B, on ne peut pas nécessairement aller de B à A sauf si une autre arête allant de B à A existe.

Propriétés des graphes orientés :

Sommets (noeuds) : les éléments ou entités distinctes du graphe.
Arêtes orientées (arcs) : les connexions entre les sommets qui ont une direction.
Degré d'entrée : le nombre d'arêtes entrantes dans un sommet.
Degré de sortie : le nombre d'arêtes sortantes d'un sommet.
Chemin : une séquence d'arêtes qui permet de passer d'un sommet à un autre.

Représentation en Python :

Il existe plusieurs façons de représenter un graphe orienté en Python :

Liste d'adjacence : Un dictionnaire où chaque clé est un sommet, et la valeur associée est une liste de sommets adjacents (c'est-à-dire ceux vers lesquels une arête pointe).
Matrice d'adjacence : Une matrice (ou tableau 2D) où l'entrée à la ligne i et la colonne j indique la présence ou l'absence d'une arête du sommet i vers le sommet j.

Exemple avec une liste d'adjacence :

Voici un exemple simple de graphe orienté utilisant une liste d'adjacence en Python :

🐍 Editeur

# Représentation d'un graphe orienté avec une liste d'adjacence
graphe = {
    'A': ['B', 'C'],
    'B': ['C', 'D'],
    'C': [],
    'D': ['C']
}

print("Graphe orienté :")
for nooeud, aretes in graphe.items():
    print(f"{noeud} -> {aretes}")

Explication :

Le sommet 'A' a des arêtes vers 'B' et 'C'. Le sommet 'B' a des arêtes vers 'C' et 'D'. Le sommet 'C' n'a pas d'arêtes sortantes. Le sommet 'D' a une arête vers 'C'.

Exemple avec une matrice d'adjacence :

Voici comment on peut représenter le même graphe avec une matrice d'adjacence :

🐍 Editeur

# Représentation d'un graphe orienté avec une matrice d'adjacence
# Les sommets sont A, B, C, D et sont indexés comme 0, 1, 2, 3 respectivement
matrice = [
    [0, 1, 1, 0],  # A -> B, C
    [0, 0, 1, 1],  # B -> C, D
    [0, 0, 0, 0],  # C -> (rien)
    [0, 0, 1, 0]   # D -> C
]

print("Matrice d'adjacence :")
for ligne in matrice:
    print(ligne)

Explication :

La première ligne [0, 1, 1, 0] indique que le sommet 'A' (index 0) a des arêtes vers 'B' (index 1) et 'C' (index 2). La deuxième ligne [0, 0, 1, 1] indique que le sommet 'B' (index 1) a des arêtes vers 'C' (index 2) et 'D' (index 3), etc.

Conclusion :

Les graphes orientés sont des structures de données très flexibles et puissantes utilisées dans de nombreux domaines tels que les réseaux, les modèles de flux, les algorithmes de recherche, etc. Python offre plusieurs façons de les représenter et de les manipuler, les plus courantes étant les listes d'adjacence et les matrices d'adjacence.