Récursivité

Présentation⚓︎

Principe de la récursivité⚓︎

Définition

La récursivité est une technique en programmation où une fonction s'appelle elle-même pour résoudre un problème.

Cela permet de décomposer un problème complexe en sous-problèmes plus simples, souvent identiques à la structure du problème original.

La récursivité repose sur deux éléments essentiels :

Cas de base (ou condition d'arrêt) : C'est la condition qui arrête la récursion. Sans cela, la fonction continuerait à s'appeler indéfiniment, entraînant un dépassement de la pile d'exécution. Le cas de base est généralement le problème le plus simple possible, dont la solution est immédiate.
Appel récursif (ou cas général) : C'est la partie de la fonction où elle s'appelle elle-même, mais avec des arguments modifiés pour se rapprocher progressivement du cas de base.

Exemple : Fonctions factorielle récursive et itérative

Fonction factorielle récursiveAnalyse avec PythontutorFonction factorielle itérative

Évaluations restantes : ∞/∞

Choix : fonction récursive ou itérative ?⚓︎

Différences entre fonction récursive et fonction itérative

Les fonctions récursives et fonctions itératives sont deux approches différentes pour résoudre un problème, et chacune présente des avantages et des inconvénients.

Fonction récursive

Une fonction récursive est une fonction qui s'appelle elle-même pour résoudre un problème en le décomposant en sous-problèmes plus petits jusqu'à atteindre un cas de base. Chaque appel de la fonction crée une nouvelle entrée dans la pile d'exécution.

Avantages :

Simplicité : Certaines tâches, comme le traitement des arbres ou des structures hiérarchiques, sont plus intuitives à résoudre de manière récursive.
Modularité : Le code est souvent plus élégant et plus simple à comprendre pour des problèmes qui se décomposent naturellement en sous-problèmes similaires.

Inconvénients :

Risque de dépassement de la pile (stack overflow) : Chaque appel récursif utilise de la mémoire, et une récursion trop profonde peut entraîner un dépassement de la pile d'exécution si la mémoire allouée est épuisée.
Performance : Les fonctions récursives peuvent être plus lentes que les fonctions itératives en raison du coût des appels successifs et de la gestion de la pile d'appels.

Fonction itérative

Une fonction itérative utilise des boucles (comme for ou while) pour répéter des opérations jusqu'à ce qu'une condition soit remplie. L'itération n'utilise pas la pile d'exécution pour stocker les états intermédiaires, mais repose plutôt sur des variables pour maintenir les informations nécessaires.

Avantages :

Meilleure gestion de la mémoire : L'itération n'utilise pas la pile d'exécution, donc il n'y a pas de risque de dépassement de la pile, même pour des problèmes plus grands.
Performance améliorée : Les boucles sont souvent plus rapides car elles ne nécessitent pas le coût supplémentaire des appels de fonction successifs.

Inconvénients :

Complexité : Pour certains problèmes (comme les structures de données récursives), une solution itérative peut être plus difficile à écrire et à comprendre.
Moins naturel : Certains problèmes sont plus naturellement résolus par la récursion. Essayer d'adopter une approche itérative peut rendre le code moins lisible ou plus complexe.

Exemple : suite de Fibonacci⚓︎

Cette célèbre suite inventée par le mathématicien italien Leonardo Fibonacci (1170-1250) est définie par récurrence de la manière suivante :

\[ \begin{aligned} F_0 &= 0, \\ F_1 &= 1, \\ F_n &= F_{n-1} + F_{n-2} \quad \text{pour} \quad n \geq 2. \end{aligned} \]

Autrement dit, chaque terme de la suite est la somme des deux termes précédents.

Fonctions récursive et itérative pour calculer les termes de la suite de Fibonacci

Fonction fibo1 récursiveFonction fibo_iter itérativeComparaisonComplexités des fonctions

Évaluations restantes : ∞/∞

Le temps de calcul de la fonction récursive fibo1 devient vite très grand alors qu'il reste raisonnable pour la fonction itérative fibo2 et même pour des grandes valeurs de n !

Complexités de `fibo1` (fonction récursive) :⚓︎

Complexité temporelle : $O(2^n)$

Le temps d'exécution croît de façon exponentielle à mesure que $n$ augmente, en raison de la duplication des calculs dans la récursion.
Complexité spatiale : $O(n)$

L'espace mémoire requis est proportionnel à la profondeur maximale de la pile d'appels, soit $n$.

Complexités de `fibo2` (fonction itérative) :⚓︎

Complexité temporelle : $O(n)$

Chaque itération se fait en temps constant, et la boucle s'exécute $(n−1)$ fois.
Complexité spatiale : $O(1)$

La fonction utilise un nombre constant de variables (principalement $a$, $b$, $i$), donc l'espace mémoire requis ne dépend pas de $n$.

Tableau comparatif⚓︎

Tableau comparatif

Critère	Fonction récursive	Fonction itérative
Simplicité du code	Souvent plus simple pour des problèmes récursifs	Plus complexe dans certains cas
Utilisation de la mémoire	Utilise la pile d'exécution pour stocker les appels	Utilise des variables locales sans surcharge de la pile
Risque de dépassement	Peut provoquer un dépassement de pile pour des cas très profonds	Pas de risque de dépassement de pile
Performances	Peut être plus lente en raison des appels successifs	Généralement plus rapide pour des problèmes simples
Cas d'utilisation	Structures arborescentes, problèmes récursifs naturels	Problèmes simples, boucles, tâches répétitives

Critères de choix⚓︎

Quand choisir l'une ou l'autre ?

Récursion :
- Utilisez la récursion lorsque le problème est naturellement récursif ou se décompose facilement en sous-problèmes plus petits (ex : traversée d'un arbre, algorithmes de tri comme quicksort et mergesort).
- Utilisez-la également lorsque la simplicité et la lisibilité du code sont des priorités, et que la profondeur de la récursion est raisonnable.
Itération :
- Utilisez l'itération lorsque vous devez résoudre des problèmes nécessitant de nombreuses répétitions (boucles) et où la performance et l'efficacité mémoire sont importantes.
- L'itération est également préférable si vous craignez un dépassement de la pile pour des problèmes nécessitant beaucoup d'étapes ou une grande profondeur.

Vidéos de Cédric Gerland (lycée Saint-Exupéry de Mantes-la-Jolie)⚓︎

Les fonctions récursives - Applications Python - Calcul de puissance (09:33)

Fonctions récursives en Python - Suite de Fibonacci - Flocon de Koch (18:21)

Les tours de Hanoï - Fonctions récursives avec Python - Python Tutor (16:03)

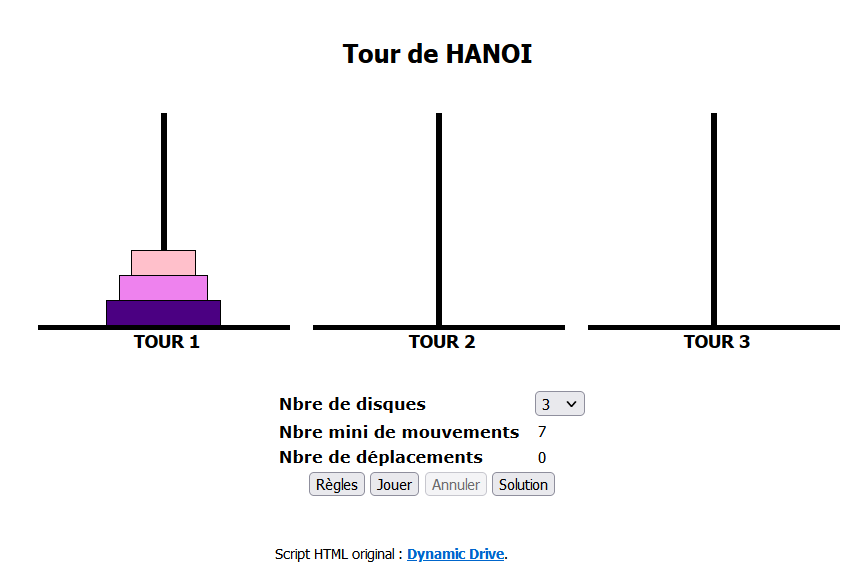
Tour de Hanoï⚓︎

Jeu en ligne⚓︎

Jeu de la tour de Hanoï (en ligne)

Récursion et tours de Hanoï⚓︎

Récursion - Tours de Hanoï | Christian Queinnec (13:27)

La tour de Hanoï, entre jeu, algorithmes et fractales⚓︎

La tour de Hanoï, entre jeu, algorithmes et fractals | Benoît Rittaud (13:165)

$Cliquer pour voir la vidéo : La tour de Hanoï, entre jeu, algorithmes et fractals | Benoît Rittaud$

Carrés imbriqués⚓︎

🐍 Editeur

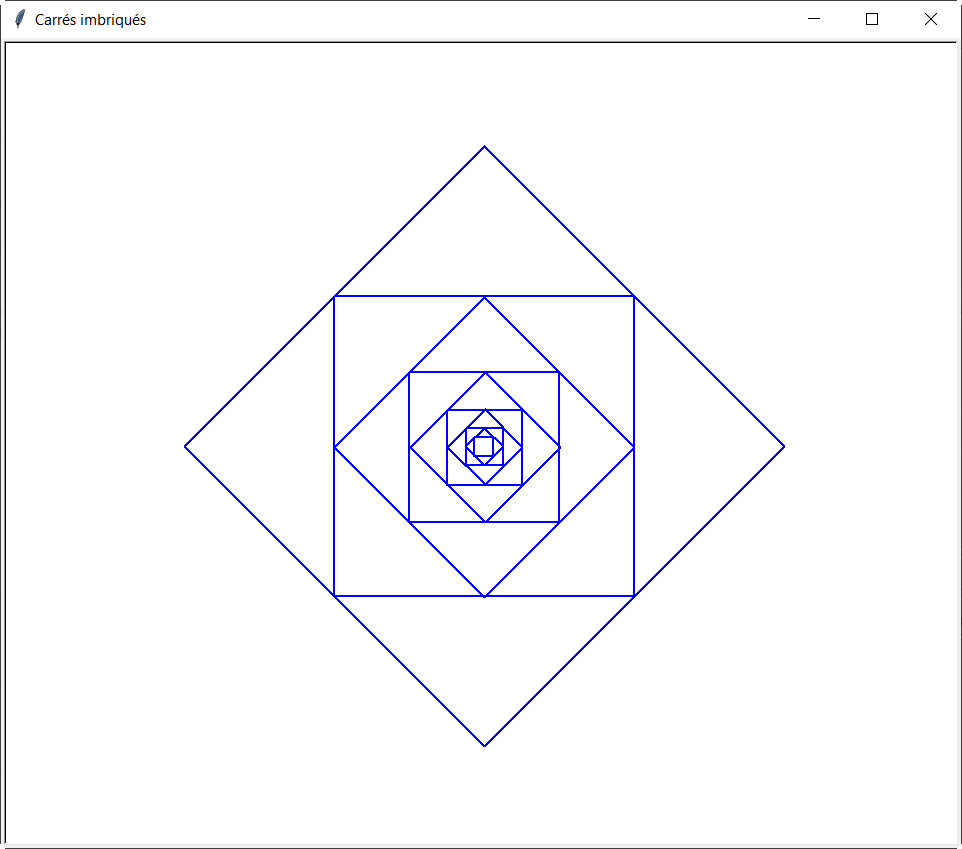
from turtle import *


def carre(cote):
    """Trace un carré de côté 'cote'"""
    for _ in range(4):
        forward(cote)
        left(90)


def imbrique(cote, n):
    """n carrés imbriqués"""
    if n >= 0:
        carre(cote)  # trace un carre de côté 'cote'
        penup()  # stylo relevé
        forward(cote // 2)  # placement au milieu d'un côté
        left(45)  # direction d'une diagonale
        pendown()  # stylo abaissé
        imbrique(cote / 2**0.5, n - 1)  # appel récursif avec côté / racine(2)


title("Carrés imbriqués")  # titre de la fenêtre graphique
hideturtle()  # pointeur caché pour ne visualiser que le tracé
speed(0)  # vitesse maximale
pencolor("blue")  # couleur du tracé
width(2)  # épaisseur du trait

cote = 600
penup()
goto(-cote // 2, -cote // 2)  # centrer la figure par rapport à l'origine
nb_carres = 10
imbrique(cote, nb_carres)

exitonclick()  # fermeture de la fenêtre en cliquant

Récursivité (doc. Eduscol)⚓︎

Fichier PDF

Récursivité

Présentation⚓︎

Principe de la récursivité⚓︎

Choix : fonction récursive ou itérative ?⚓︎

Exemple : suite de Fibonacci⚓︎

Complexités de fibo1 (fonction récursive) :⚓︎

Complexités de fibo2 (fonction itérative) :⚓︎

Tableau comparatif⚓︎

Critères de choix⚓︎

Vidéos de Cédric Gerland (lycée Saint-Exupéry de Mantes-la-Jolie)⚓︎

Tour de Hanoï⚓︎

Jeu en ligne⚓︎

Récursion et tours de Hanoï⚓︎

La tour de Hanoï, entre jeu, algorithmes et fractales⚓︎

Carrés imbriqués⚓︎

Récursivité (doc. Eduscol)⚓︎

Complexités de `fibo1` (fonction récursive) :⚓︎

Complexités de `fibo2` (fonction itérative) :⚓︎